A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in the major segment.
Answer:
30°
- Look at the image below:
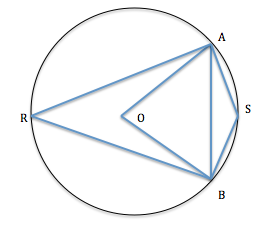
The chord AB has a length equal to the radius of the circle.
This means that ΔOAB is an equilateral triangle. (all the sides and angels are equal and each angle measure 60°)
So, ∠AOB = 60°. - We know that the angle subtended by a chord at the center is twice the angle subtended by the chord at a point in the major segment.
Consider a point R on the major segment.
∠AOB = 2∠ARB.
Therefore, ∠ARB = 30°
 Bangladesh
Bangladesh
